GRÁFICO DE FUNÇÕES

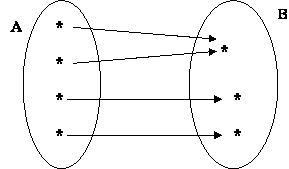
Pode-se representar graficamente uma função usando vários tipos de gráficos: gráficos de barras, correspondência ou relação entre conjuntos, gráfico cartesiano.

O gráfico cartesiano permite a visualização da forma e do comportamento da função. Para representar uma função no gráfico cartesiano, identifica-se um conjunto de pontos pertencentes á função.
Cada ponto pertence a uma coordenada (x,y), de modo que satisfaçam a função determinada, tal que obtemos que (x,f(x)).

Considerando f como a função de um conjunto M para um conjunto N. O gráfico de f é dito como o conjunto de pares ordenados {(m,n) | m E M e f(m) = N}

O gráfico de uma função f de M para N, é dito o subconjunto M x N que contém os pares ordenados com a segunda entrada igual a um elemento de N determinado por f para a primeira entrada.
Deve-se sempre prestar atenção ao domínio da função.

Exemplo:  fR→R com f(x) = x². Os pares ordenados são obtidos por (x,x²). Plotando os pares num plano cartesiano, observamos que o gráfico ficará da seguinte forma:

Exercícios: Esboce os gráficos das seguintes funções:

a) fR→R com f(x) = x³

b) f(x) = x , com f E Z+

c) fR→R com f(x)= x²/2

INTRODUÇÃO A FUNÇÕES

Definição: Sejam X e Y conjuntos não vazios. Uma função de X para Y é uma determinação de exatamente um elemento de X para cada elemento de Y.

Elas também podem ser chamadas de mapeamentos ou transformações.

Funções são escritas da seguinte forma:   f(x) = y   ou  X -> Y .

Para compreender melhor o que são funções deve-se, primeiramente, introduzir alguns conceitos como domínio, contradomínio, imagem e pré-imagem.

Se f é uma função de X para Y, dizemos que X é o domínio de f e Y é o contradomínio de f. Se f(x) = y, dizemos que y é a imagem de x e que a x é a pré-imagem de y. O conjunto imagem de f é o conjunto de todas as imagens e elementos de x. Assim como está representado na figura abaixo.

Para que uma função seja completa ela precisa de seu domínio e de seu contradomínio, assim como de uma associação entre eles, que pode ser fornecida por meio de gráfico, descrição verbal, equação ou coleção de pares ordenados.

Igualdade de funções: acontece quando elas possuem o mesmo domínio, o mesmo contradomínio e a mesma associação de valores do contradomínio a valores do domínio.

FUNÇÕES INVERSAS

Considere uma função f bijetora no conjunto A para o conjunto B. Como f é uma função sobrejetiva, todo elemento de B é a imagem de um único elemento no conjunto A. Consequentemente, podemos definir uma nova função de B para A que inverte a correspondência dada por f.

Define-se uma função inversa como: Seja f uma função bijetora do conjunto A para o conjunto B. A função inversa de f é a função que leva a um elemento b, que pertence a B, o único elemento a no conjunto A, tal que f(a)=b. A função inversa de f é indicada por f^-1. Assim, f^-1(b)=a quando f(a)=b.  

Deve-se policiar para não confundir a função f^-1 com a função 1/f, que é a função que toma para cada x do domínio o valor 1/f(x). Note que esta ultima só faz sentido quando f(x) é um número real diferente de zero. Essas duas funções f^-1 e 1/f não são iguais.

Se uma função f não é uma bijeção, não podemos definir uma função inversa de f. Quando f não é uma bijeção, ela não é injetora ou não é sobrejetiva. Se f não é injetora, algum elemento b do contradomínio é a imagem de mais de um elemento do domínio. 

Se f não é sobrejetiva, para algum elemento b do contradomínio, não existe um elemento a no domínio para que f(a)=b. Consequentemente, se f não é uma bijeção, não podemos determinar para cada elemento b do contradomínio um único elemento a do domínio, tal que f(a)=b (porque para algum b há mais de um elemento a ou não há projeção para a).

Uma bijeção é chamada de inversível, pois podemos definir uma função inversa. Uma função é não-inversível se não é uma bijeção, porque não existe a função inversa.

Execícios:

COMPOSIÇÃO DE FUNÇÕES

Considere g  como uma função do conjunto A para o conjunto B e considere f  como uma função do conjunto B para o conjunto C. A composição das funções f e g,  indicada por f o g, é definida por:

(f o  g) = (f(g(a)).

Para encontrar (f o g)(a),  primeiro aplicamos a função g em a para obter g(a) e, então, aplicamos a função f  ao resultado g(a) para obter (f o g)(a) = f(g(a)).

Exercício: utilizar funções f e g e obter a composição de f com g e de g com f.

Sendo f(x) = 4x-5 e g(x) = 3x²+2.

(Primeiramente obter (f º g) (x) , depois (g º f) (x) :

 Neste caso você pode constatar que (f º g) (x) é diferente de (g º f) (x).

FUNÇÕES INJETORAS

Funções injetoras são aquelas que nunca determinam o mesmo valor para dois elementos diferentes do domínio.

Definição: Uma função f é chamada de injetora, se e somene se f(a) = f(b) implica que a = b para todos os a e b no domínio de uma f. Uma função pode ser chamada de injeção se for de um para um.

Utilizando quantificadores, é possível expressar uma função injetora como Va Vb (f(a) = f­(b) → a = b) ou, equivalentemente Va Vb (a ≠ b → f(a) ≠ f­(b)), em que o universo do discurso é o domínio da função.

Para melhor compreensão, as figuras abaixo indicam exemplos e contraexemplos de funções injetoras:

                                                          Figura 1 - Função Injetora

O diagrama apresentado na Figura 1 mostra uma função injetora em que f(a) ≠ f­(b) → a ≠ b em f: A → B.

Figura 2 - Função não injetora

O diagrama apresentado na Figura 2 mostra uma função não injetora f: A → B, pois determina o mesmo valor para dois elementos do domínio.

Graficamente, podemos analisar em funções f: R → R da seguinte maneira:

Figura 3 - Gráfico de uma função injetora

Figura 4 - Gráfico de uma função não injetora

Exemplo 1: Se determinarmos uma função f de {a, b, c, d} para {1, 2, 3, 4, 5} com f(a) = 4, f(b) = 5, f(c) = 1 e f(d) = 3. Podemos concluir que a função f é injetora, pois f assume valores distintos para os elementos no seu domínio. O diagrama dessa função pode ser ilustrado na figura abaixo.

Função

Função Sobrejetora

Uma função f é dita sobrejetora se todos os elementos do conjunto co-domínio(imagem) estiverem associados a elementos do conjunto domínio, ou seja , o conjunto imagem de f , for igual ao conjunto co-domínio de f : ∀y ∈ Y,∃x ∈ X | y = f(x) .As funções das Figuras  1 e 2 não são sobrejetoras. A Figura 3 ilustra uma função sobrejetora.

                                            

Figura 1:Função não sobrejetora

Figura 2: Função não sobrejetora

 Figura 3: Função sobrejetora

a) A função f: R -> R definida por f(x)=3x+2 é sobrejetora, pois todo número real é imagem de algum número real pela função f.

b) A função f: R -> R+ definida por f(x)=x² é sobrejetora, pois todo elemento pertencente a R+ é imagem de pelo menos um elemento de R  pela função.

Observação: R+ = {x e R | x>=0}, ou seja, conjunto dos reais não negativos.

                  

c)A função f: Z -> Z+ definida por f(x)=x² é sobrejetora, pois todo numero inteiro positivo é imagem de algum número inteiro pela função f.

Referencias

           http://uab.ifsul.edu.br/tsiad/conteudo/modulo1/mat/mat_ud/mat_ud04.html

           http://pt.slideshare.net/UlrichSchiel/matemtica-discreta-parte-vi-funes  

           http://www.inf.ufsc.br/~santana/ine5403/notas_de_aula/notas/p71funcoesf.pdf