Função

Função Sobrejetora

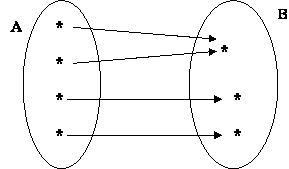
Uma função f é dita sobrejetora se todos os elementos do conjunto co-domínio(imagem) estiverem associados a elementos do conjunto domínio, ou seja , o conjunto imagem de f , for igual ao conjunto co-domínio de f : ∀y ∈ Y,∃x ∈ X | y = f(x) .As funções das Figuras  1 e 2 não são sobrejetoras. A Figura 3 ilustra uma função sobrejetora.

                                            

Figura 1:Função não sobrejetora

Figura 2: Função não sobrejetora

 Figura 3: Função sobrejetora

a) A função f: R -> R definida por f(x)=3x+2 é sobrejetora, pois todo número real é imagem de algum número real pela função f.

b) A função f: R -> R+ definida por f(x)=x² é sobrejetora, pois todo elemento pertencente a R+ é imagem de pelo menos um elemento de R  pela função.

Observação: R+ = {x e R | x>=0}, ou seja, conjunto dos reais não negativos.

                  

c)A função f: Z -> Z+ definida por f(x)=x² é sobrejetora, pois todo numero inteiro positivo é imagem de algum número inteiro pela função f.

Referencias

           http://uab.ifsul.edu.br/tsiad/conteudo/modulo1/mat/mat_ud/mat_ud04.html

           http://pt.slideshare.net/UlrichSchiel/matemtica-discreta-parte-vi-funes  

           http://www.inf.ufsc.br/~santana/ine5403/notas_de_aula/notas/p71funcoesf.pdf